Scoliose chaotique et scoliose linéaire

 La première publication concernant la théorie du chaos date de mon livre publié en 1986. Une approche mathématique a été présentée en 2012.

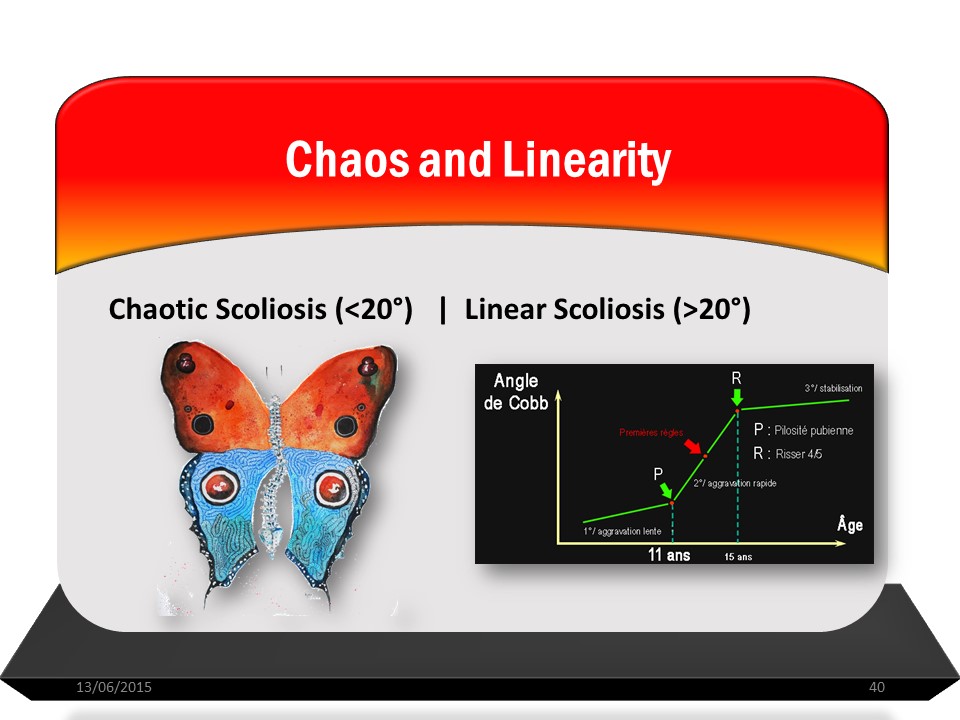 Il existe en effet 2 modes évolutifs de scoliose. La scoliose linéaire de plus de 25° avec le cercle vicieux en période d'adolescence et la scoliose chaotique de moins de 20° pour laquelle il est impossible d'établir un pronostic évolutif.

 Nous allons étudier plus en détail les caractéristiques d'un système chaotique.

 Dans un système non chaotique (comme un simple pendule), changer légèrement l'état initial ne conduit qu'à un léger changement dans la façon dont le système se développe. Par exemple, si le pendule simple partait d'une position légèrement plus élevée que celle illustrée ici, il se déplacerait sur un arc qui n'est que légèrement plus long avec une vitesse qui n'est que légèrement plus grande, mais les trajectoires globales seraient presque les mêmes. Par contre, si vous modifiiez légèrement la position initiale du double pendule, cela conduirait à une trajectoire complètement différente de celle illustrée ici, et c'est la propriété la plus importante d'un système chaotique: tout changement (même minime) dans l'état initial du système conduit à un développement complètement différent du système après un certain temps. Une scoliose de plus de 25 ° évoluera toujours selon les lois de Duval Beaupère. Les résultats des traitements sont relativement homogènes. Une scoliose de moins de 25 ° évoluera comme le double pendule et un petit changement initial pourra entraîner un pronostic totalement différent. Ceci est fondamental pour la physiothérapie.

 La scoliose est la matérialisation concrète de la théorie du chaos appliquée à la colonne vertébrale. Le système est: Ouvert (position debout, échange avec l'extérieur), non prédictif (effet papillon), complexe (multifactoriel), discontinu (étapes), Déterministe (pas par chance), Modélisable (4ème dimension fractale), avec un attracteur étrange, et changement de comportement physiologique à la puberté.

 L'impossibilité de prédire l'évolution de la scoliose à ce stade est l'effet papillon bien décrit par Edward Lorentz: «Est-ce que le battement d'ailes d'un papillon au Brésil peut créer une tornade au Texas?».

 La pomme tombe selon la loi de gravitation de Newton, et on peut prévoir le lieu de la chute. La feuille d'arbre tombe selon les mêmes lois, mais nous ne pouvons pas prévoir le lieu exact de la chute, car elle est plus sensible au vent. L'imprévisibilité de tels phénomènes est liée à une extrême sensibilité aux conditions initiales, c'est le chaos déterministe.

 Si un flocon de neige peut provoquer une avalanche, la prévision par calcul pourait nous dire exactement quel flocon de neige précis doit être intercepté pour l'avalanche ne se produise pas. En fait dans un système chaotique un état supercritique reste un état supercritique, et supprimer ce flocon de neige particulier ne permettrait qu'à un autre de le remplacer dans cette fonction. Rien ne serait résolu.

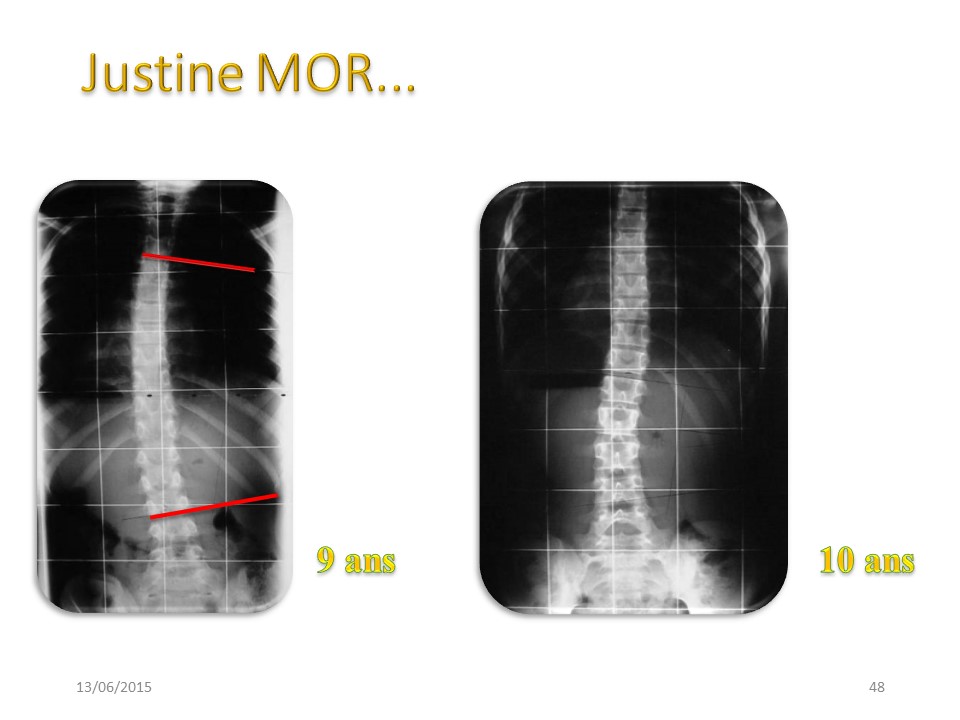 Nous voyons fréquemment en consultation des scolioses inférieures à 20° se corriger totalement au contrôle suivant sans aucun traitement particulier. C'est pourquoi il est très difficile d'affirmer l'efficacité de la kinésithérapie pour ce type de scoliose.

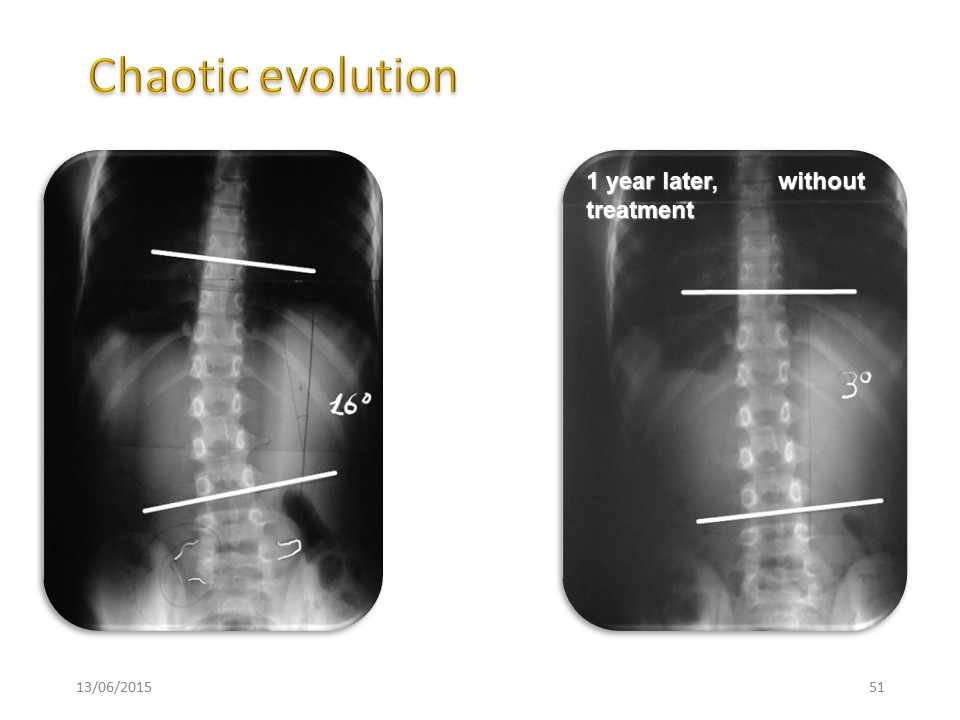 Un autre exemple d'évolution chaotique sans aucun traitement.

 L'existence d'un attracteur étrange a été décrite par un mathématicien français. La moyenne de tous les mouvements du rachis au cours de la journée, n'est plus une colonne droite, mais une colonne incurvée.

 Un système chaotique est toujours un système complexe comme le double pendule.

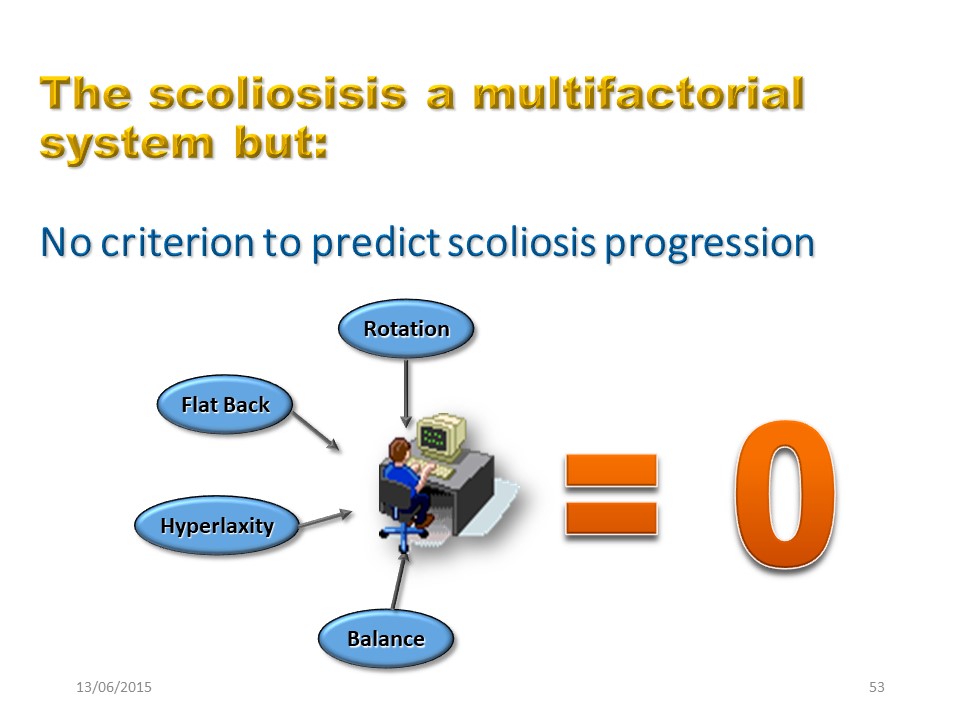 L'étiologie de la scoliose est multifactorielle et complexe. Lorsque nous rassemblons dans un ordinateur les différentes caractéristiques d'une scoliose évolutive: le dos plat, la rotation, l'hyperlaxité et la perturbation de l'équilibre ... La réponse est négative: aucune de ces caractéristiques ne permet de prédire l'évolution de la scoliose. Seul un angle supérieur à 25 ° est caractéristique de la scoliose progressive, mais nous ne sommes plus dans une phase de chaos.

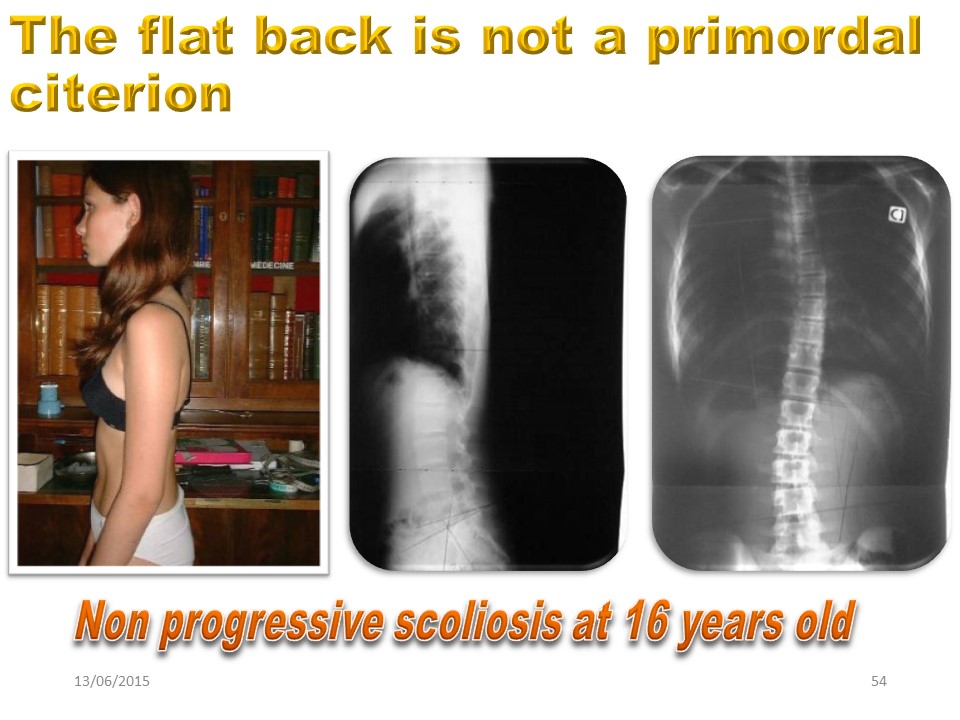 Par exemple, nous voyons souvent un dos plat dans la scoliose très évolutive, mais l'inverse n'est pas vrai. Cet enfant présente un important dos plat, mais quasiment pas de scoliose en fin de croissance staturale.

 Le paradoxe de la théorie du chaos est que la scoliose survient très fréquemment chez un enfant "normal". Actuellement, nous voyons souvent des scolioses évolutives avec des troubles posturaux que nous avons étudiés dans la chapitre étiologique. Mais un déséquilibre majeur tel que l'hémiplégie infantile ne provoquera que 10% de scolioses évolutives.

 Les mères associent souvent la scoliose à une posture asymétrique avec le cartable, ce qui est possible dans un système chaotique comme le vol du papillon au Brésil, même si la scoliose évolutivee ne concerne pas toujours les enfants présentant une asymétrie majeure. La coexistence de deux systèmes de progression chaotique et linéaire est l'une des caractéristiques de la scoliose.

 L'existence de seuils est également la caractéristique de la scoliose. Nous avons citer le seuil de 20-25° pour la mise en place d'un corset, il existe également un seuil de 50° pour l'indication chirurgicale.

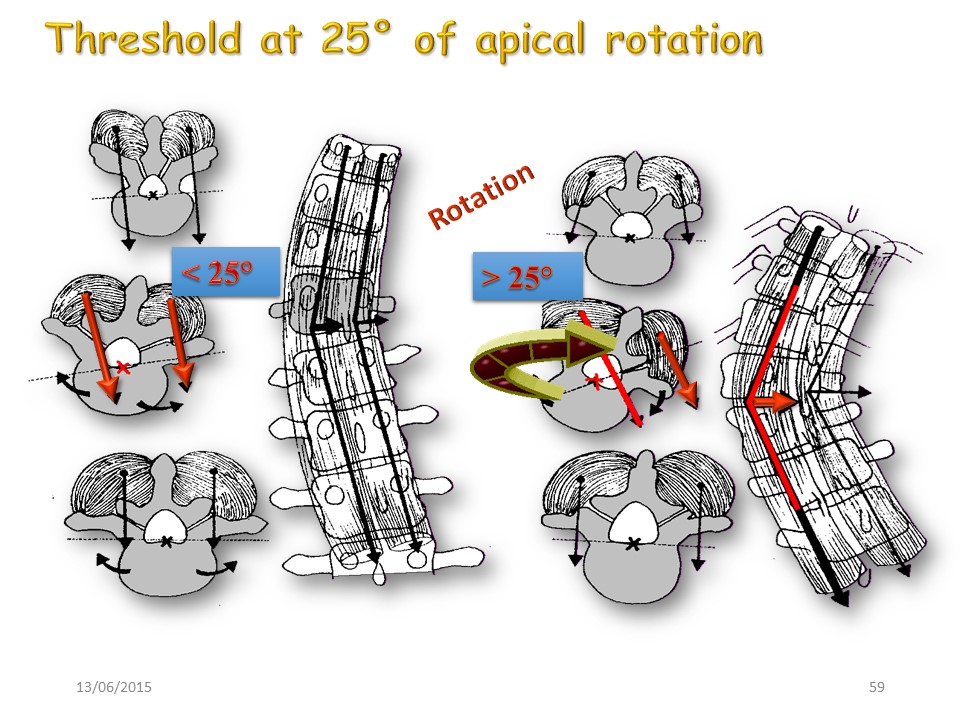 Lors d’un mouvement de flexion antérieure du tronc, une faible rotation est stable, car les bras de levier musculaire concaves et convexes se situent de part et d’autre du Centre Instantané de Rotation (mur postérieur du corps vertébral). Lorsque la rotation est plus importante, les bras de levier se situent du même côté et la vertèbre dérape comme un triporteur dans une courbe excessive.

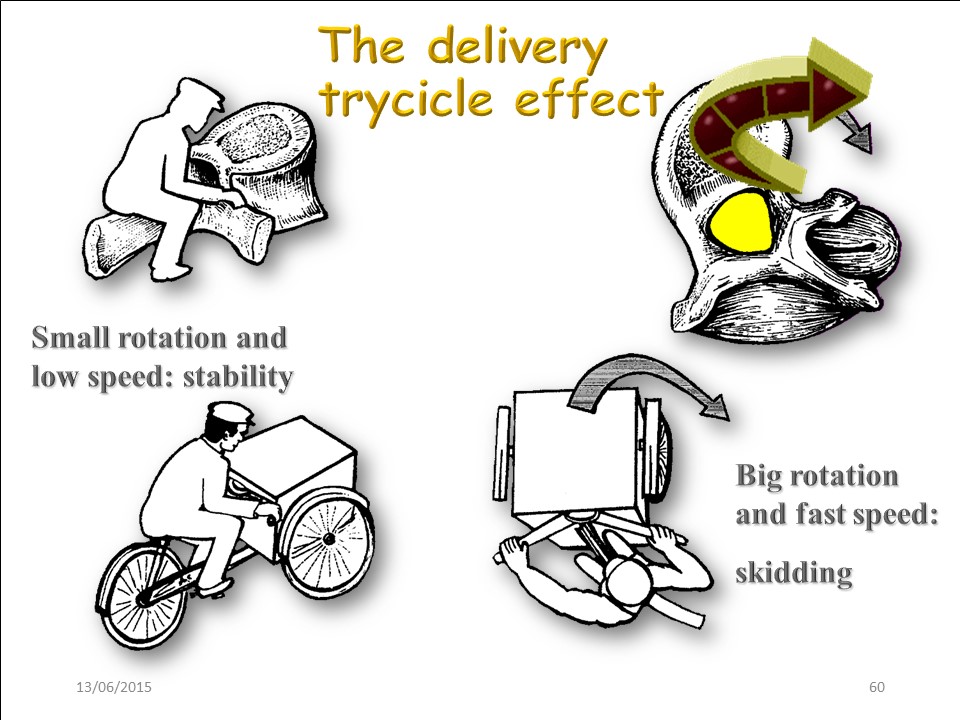 Outre la rotation apicale, une autre discontinuité peut intervenir au niveau de la vitesse. Lorsque la vitesse de la flexion antérieure du tronc est importante, la vertèbre dérape comme un trycicle de livraison dans une courbe. C'est pourquoi, le mouvement de flexion antérieure du tronc doit être effectué lentement dans la scoliose.

 Le chaos de la scoliose ne relève nullement des lois du hazard, mais de lois mathématiques complexes, c'est le chaos déterministique.

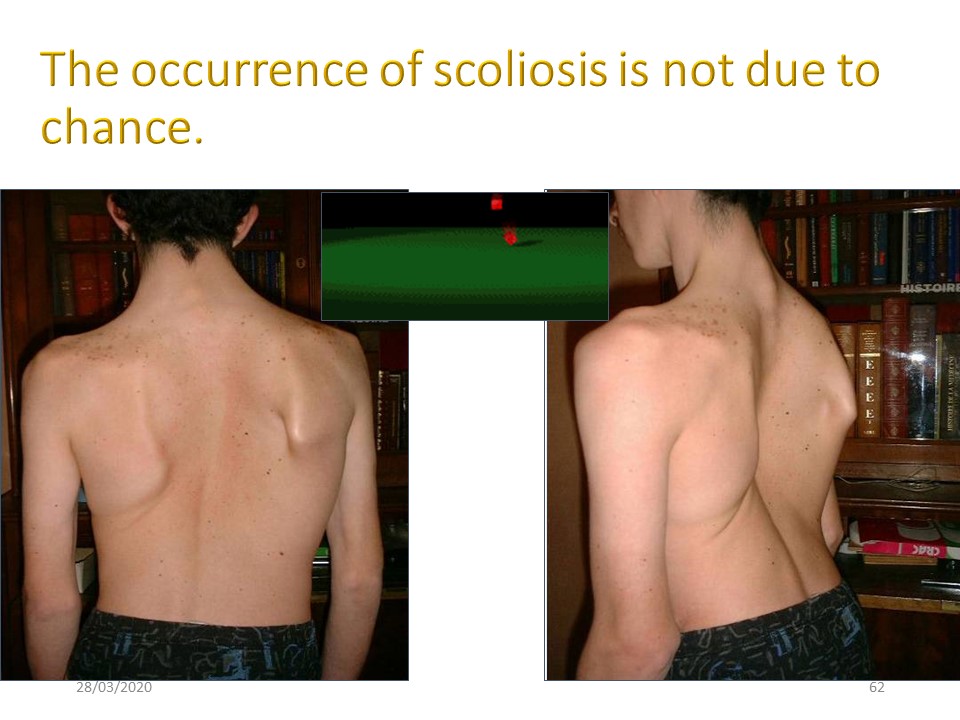 La survenue d'une scoliose ou d'un dos plat caractéristique de la scoliose n'est pas liée au hasard. Le dos plat accompagne toujours la scoliose la plus évolutive, mais nous avons vu qu'un dos plat peut exister sans scoliose.

 Le chaos déterministe est un concept qui peut offrir des réponses aux plus grands mystères de la vie. En mathématiques, informatique et physique, un système déterministe est un système dans lequel aucun hasard n'est impliqué dans le développement des futurs états du système. Un modèle déterministe produira donc toujours la même sortie à partir d'une condition de départ ou d'un état initial donné. la vérité est que la plupart des systèmes dans la nature sont chaotiques. Cela signifie notamment que, même dans le domaine de la biomécanique classique, nous ne pourrons en principe jamais simuler avec précision la réalité dans laquelle nous vivons. Quelle que soit la précision de nos appareils de mesure, nous ne pourrons jamais prédire avec précision le comportement de l'environnement dans lequel nous vivons. Les systèmes physiques sont déterministes car ils obéissent à des équations différentielles déterministes. Ils peuvent être conservateurs ou dissipatifs. De cette façon, les mesures effectuées sur l'état d'un système à un moment donné peuvent ne pas nous permettre de prédire la situation future, même à court terme, malgré le fait que les équations gouvernantes soient exactement connues. C'est le cas en météorologie. Par définition, ces équations sont nommées chaotiques lorsqu'elles prédisent un chaos déterministe.

 Ces équations que l'on nomme parfois fractales sont à l'origine des nombreuses classification que l'on retrouve dans la scoliose et qui correspondent à une discontinuité.

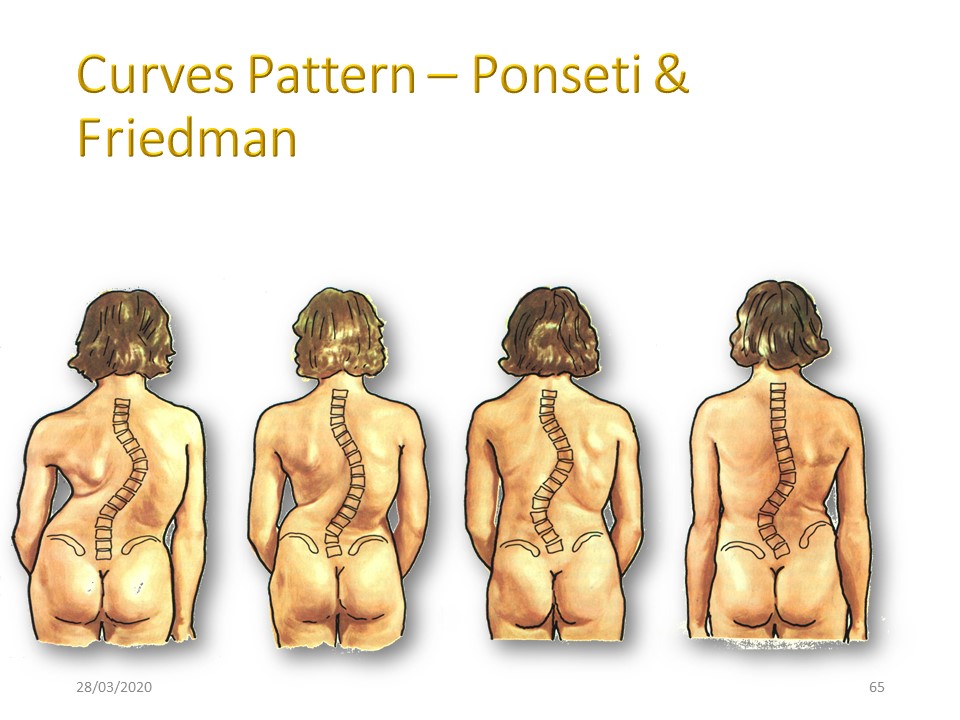 Il existe quatre types courants de courbures dans la scoliose, bien que des courbes latérales puissent apparaître n'importe où le long de la colonne vertébrale. 1, la courbe thoracique droite. Dans ce type, la scoliose majeure est concentrée dans la région thoracique et se courbe vers la droite. Il peut également y avoir une contre-courbe moins sévère vers la gauche dans le lombaire. 2, La Scoliose thoraco-lombaire droite. La courbe principale est à droite à la fois dans le thorax inférieur et la région lombaire. Ceci est communément appelé courbe en C. 3, La scoliose thoracique droite et lombaire gauche. La courbe principale se situe dans la région thoracique, avec une contre-courbe égale à gauche dans la région lombaire. Ceci est communément appelé courbe en S. (elle ressemble à un S vu de face.) 4, La scoliose lombaire gauche. La courbe principale est à gauche dans la région lombaire. Il peut y avoir une courbe moins marquée vers la région thoracique droite. Pour des raisons inconnues, depuis la latéralisation à 6 ans, la plupart des courbes thoracique sont à droite et la plupart des courbes lombaire sont à gauche. Il peut y avoir plus d'une courbe de compensation n'importe où le long de la colonne vertébrale, même dans la colonne cervicale. Pour une scoliose infantile avant la latéralisation, 50% des courbures sont à droite et 50% des courbures à gauche.

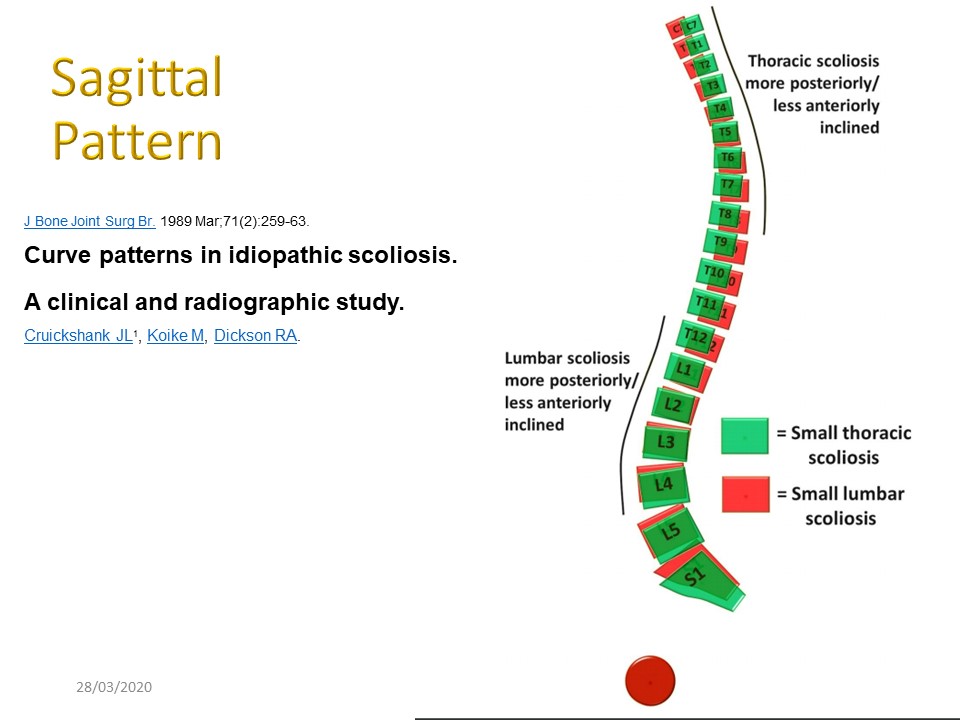 Il existe également des morphotypes sagittaux dans la scoliose. Les courbes thoraciques structurales simples ont de courtes sections lordotiques à leur sommet, limitées au-dessus et en dessous par la cyphose. Les courbes doubles ont montré des sections lordotiques plus longues limitées uniquement par une zone de cyphose. La lordose dans toute la colonne vertébrale thoracique et lombaire a été associée à des modèles de courbe triple. Il existe également une différence d'inclinaison pour les petites scolioses thoraciques en vert et les petites scolioses lombaires en rouge. La reconnaissance de la configuration des anomalies sagittales permet de concevoir le traitement sur une base anatomique solide pour des cas individuels. Cela est possible avec le plâtre digital en trois blocs.

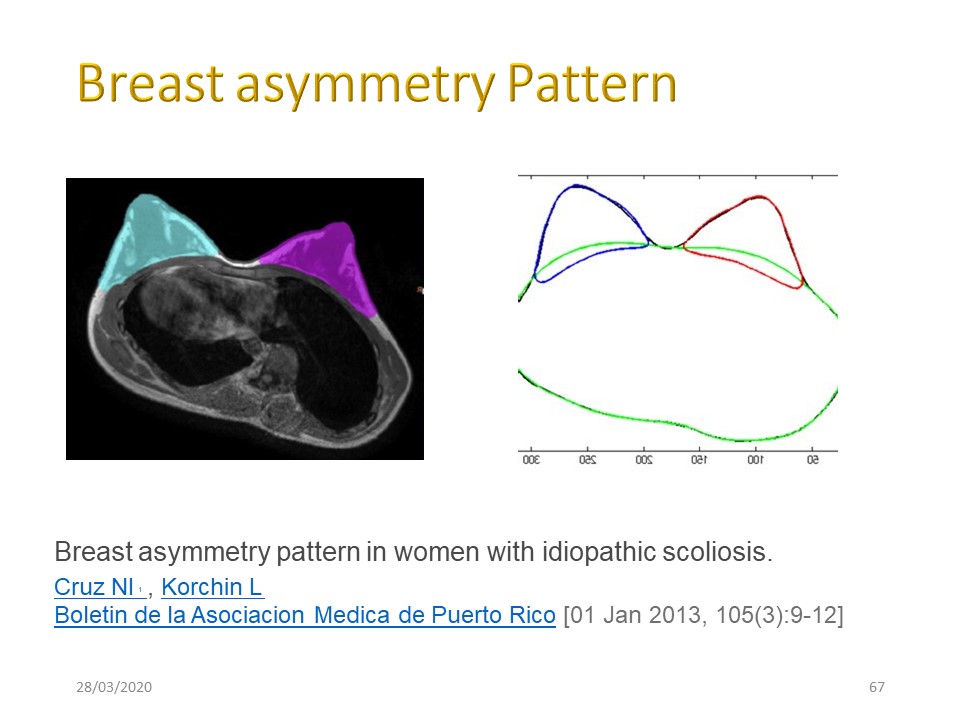 En plus de la déformation thoracique avec projection chondro-costale antérieure du côté opposé à la gibbosité, il existe également une asymétrie mammaire. Les femmes atteintes de scoliose idiopathique présentent systématiquement une asymétrie mammaire qui a suivi un schéma prévisible. Le sein sur le côté de la courbe de scoliose thoracique convexe est toujours plus petit en volume. Le côté affecté présente également une aréole plus petite, une position plus élevée du mamelon et une position plus élevée du pli inframammaire par rapport au sein opposé. Bien que l'asymétrie soit prévisible, le degré auquel le patient présente ces changements n'est pas en corrélation avec la gravité de la scoliose.

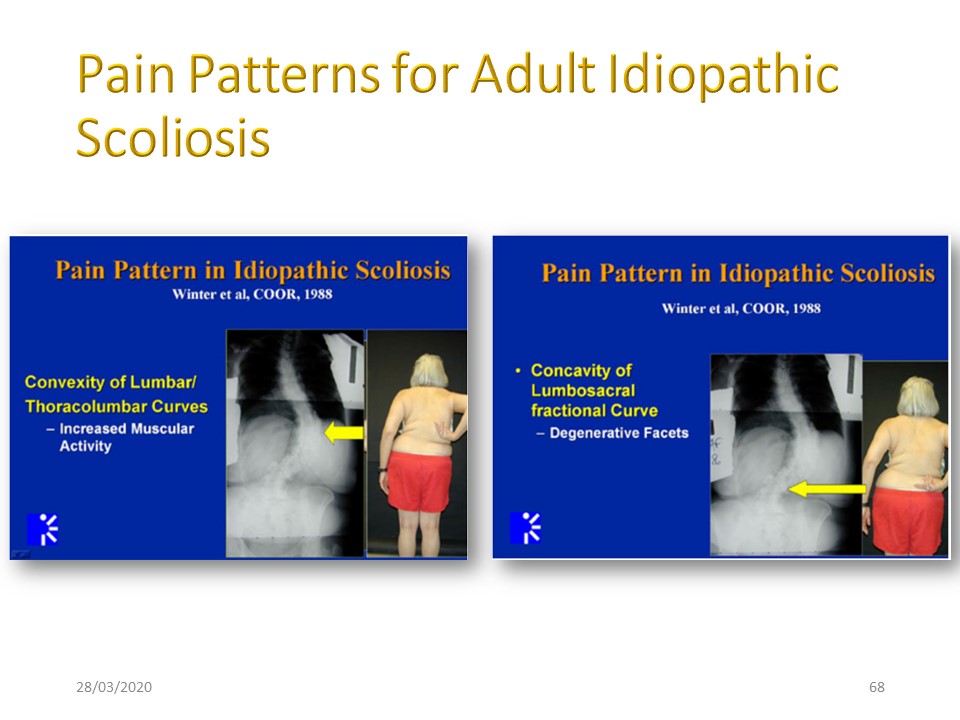 Les douleurs de scoliose idiopathique chez l'adulte sont caractéristiques. Les principales ont été décrites par Winter en 1988. La douleur de convexité est de type musculaire, la douleur de concavité est de type articulaire postérieur. Une description plus complète sera détaillée dans le module de scoliose adulte.

 La déviation scoliotique peut également être modélisée par une fractale. Une dimension fractale comprend infiniment plus d'informations qu'une dimension de coordonnées. Lorsque nous précisons l'échelle, cela nous donne la longueur.

 La 4ème dimension ou la dimension fractale de la déformation ne correspond pas aux lois de proximité dans l'espace ni à une continuité visible. C'est le chaos qui apparaît, mais en réalité les causes qui agissent les unes dans les autres sont dans une 4ème dimension. Ce qui fait pour nous le chaos, c'est que l'espace visible n'a que 3 dimensions.

 La côte bretonne a une longueur finie, mais elle a un nombre infini de longueurs, chacune correspondant à l ’échelle de mesure que l ’on choisit. Dans un système de mesure par dimension de déformation, un trajet possède un nombre infini de longueurs qui sont toutes résumées par un seul nombre.

 Fibonacci est un mathématicien du moyen age qui a introduit les chiffres arabes et le nombre zéro en Europe. La séquence trouvée dans les pétales de fleurs commence par les nombres 0,1,1,2,3,5,8,13,21,34,55 et se poursuit indéfiniment. Deux siècles plus tard; Luca Paccioli écrit "la proportion divine". Ce livre sera illustré par Léonard de Vinci. Nous retrouvons la structure triangulaire que nous avons vue dans le module de tenségrité et la spirale de Fibonacci. Ses peintures sont proportionnées selon ces principes. En fait, il y a un ordre invisible que les mathématiques permettent de voir. Si nous prenons une image radiographique d'un bras humain, cela met en avant une séquence mathématique que l'on retrouve partout dans la nature. L'humérus est relié au radius et au cubitus de l'avant-bras. L'avant-bras est relié aux 8 os du poignet. Le poignet est relié aux 5 os du métacarpien. Le métacarpe est connecté aux 3 phalanges. Ces nombres: 1, 2, 3, 5, 8 font partie de la séquence de Fibonacci. Chaque numéro est obtenu en ajoutant les deux précédents. Si nous transposons les nombres à la surface des carrés, nous obtenons un rectangle parfait appelé rectangle d'or. Si nous dessinons un arc tangent au périmètre de chaque rectangle, nous obtenons la spirale de Fibonacci. Le mouvement hélicoïdal correspond à celui d'une pomme de pin. Cette forme se trouve dans la coquille d'ammonite. Mais ce n'est pas tout. Si nous prenons un nombre de la séquence de Fibonacci et le divisons par celui qui le précède, nous obtenons un résultat proche de 1,618, qui est le nombre Phi appelé le nombre d'or. Si nous prenons l'image de la radiographie du bras. La différence de longueur entre l'avant-bras et la main est égale au nombre d'or. Cela vaut également pour les 3 phalanges, mais aussi pour notre ADN. Le rapport entre la longueur et la largeur d'un cycle complet de la double hélice de la molécule d'ADN est le nombre d'or. La séquence de Fibonacci et le nombre d'or sont des exemples d'objets fractals. La structure des nervures d'une feuille est identique à celle des branches d'un arbre. Nous avons la même forme répétée à l'infini à une échelle toujours plus petite. Une fractale est l'auto-similitude. Un motif qui peut être vu à plusieurs échelles d'observation. La nature est basée sur la géométrie fractale car elle lui permet de créer des structures gigantesques dans un volume minimum. C'est grâce à lui que le corps humain contient 96 000 km de veines et artères. Ou que 1,80 m de filament d'ADN peut être contenu dans le noyau d'une cellule. La totalité de l'ADN d'un être humain mis bout à bout, nous obtenons une longueur de 6,4 milliards de kilomètres, une distance supérieure à celle qui sépare la terre de Pluton.

 Il est étonnant de constater qu’une formule mathématique fractale fournit une image très proche de certains organes comme le cerveau, les bronches, les villosités intestinales.

 Les phénomènes chaotiques surviennent lors des changements de phase.

 Le flocon de neige qui est un intermédiaire entre l'eau liquide et la glace solide est un exemple typique d'une structure chaotique. Tous les flocons de neige sont différents, mais ils résultent tous d'une équation fractale. La valeur décimale des dimensions fractales correspond à un nombre irrationnel résultant de la division de 2 logarithmes Par exemple pour le flocon de neige dans un plan : Log 4 / Log 3 = 1,2618

 Ces images concernent essentiellement les organes qui constituent une interface entre gaz, liquides et solides. La puberté, caractéristique de l’homo sapiens, constitue en quelque sorte un changement de phase avec passage de l’enfance à l’état adulte.

 En pratique cette théorie modifie le comportement du médecin au niveau du traitement et de la prévention. Le traitement soit disant étiologique de la scoliose par un appareil dentaire ou une semelle n’a pas plus de sens que d’aller à la chasse au papillon pour éviter le tornade au Texas. Le système chaotique ne fonctionne que dans un sens. De même, si la scoliose évolue malgré la kinésithérapie, ce ne sera pas la « faute » du kinésithérapeute, pas plus que la construction antisismique ne peut éviter le tremblement de terre.

 En phase chaotique, la construction antisismique veut dire renforcer le système extrapyramidal sans changer la structure, c'est à dire sans chercher à corriger la courbure et sans réajustement des tensions.

 La déformation des voies de chemin de fer après tremblement de terre c'est à dire après un phénomène de vibrations élastiques, nous rappelle que le système postural est sensible aux vibrations.

 L’évolution des scolioses de plus de 25° est plus mécanique que posturale. Le système extra-pyramidal est dépassé et doit s'adapter en permanence à la déviation définitive du rachis.

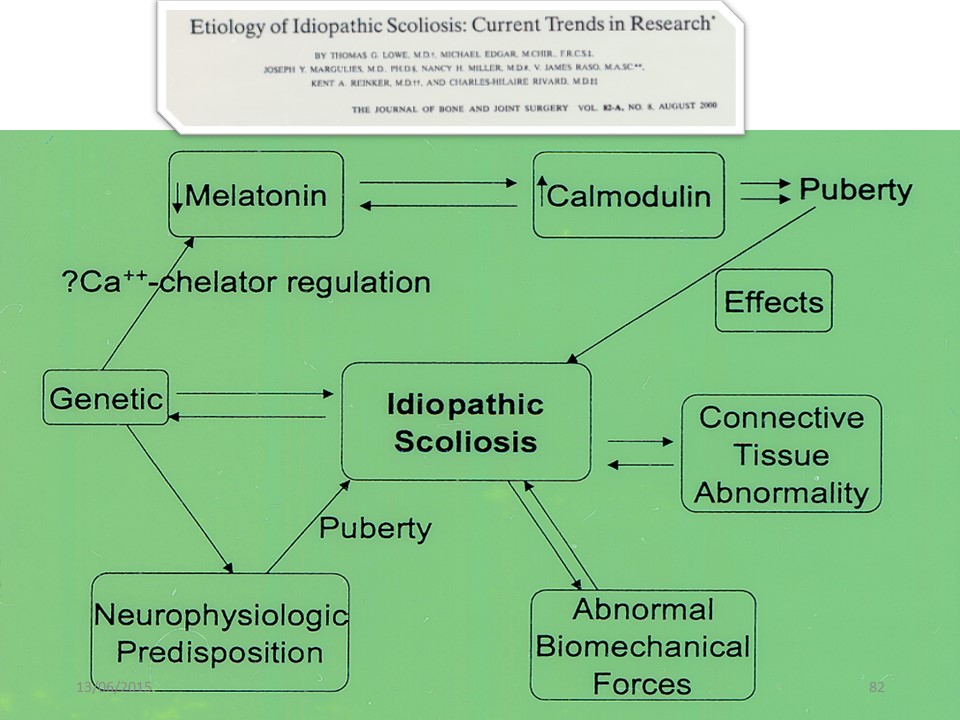 Ce sont bien les phénomènes biomécaniques anormaux qui caractérisent cette période.

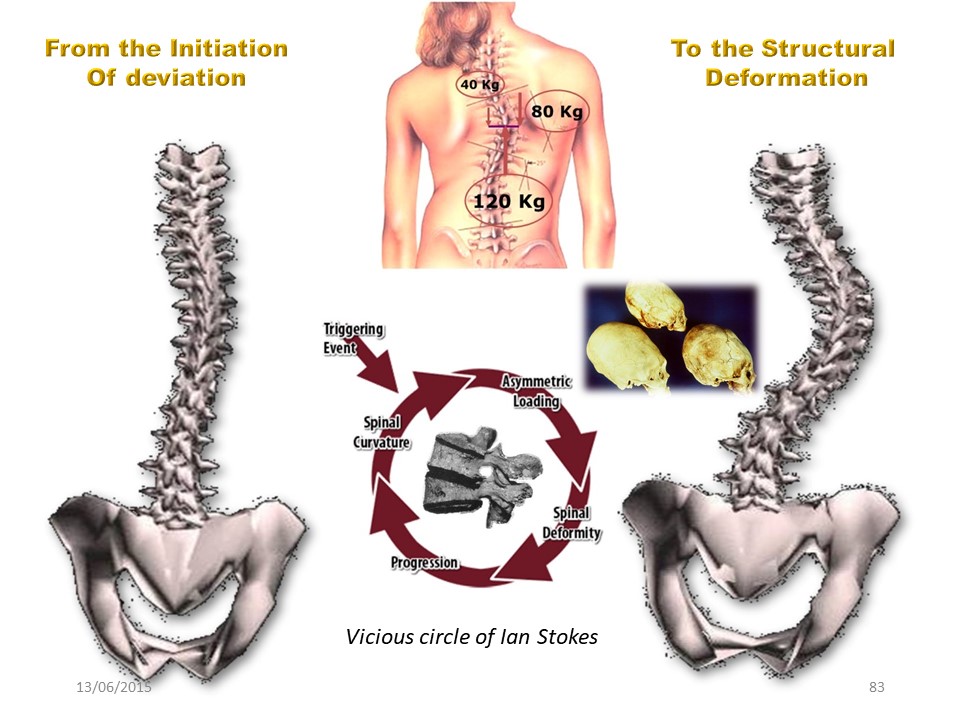 La déviation initiale devient déformation structurale avec initiation d'un cercle vicieux biomécanique décrit par Ian Stokes et accentué par la croissance pubertaire de 25 cm au niveau de la colonne vertébrale.

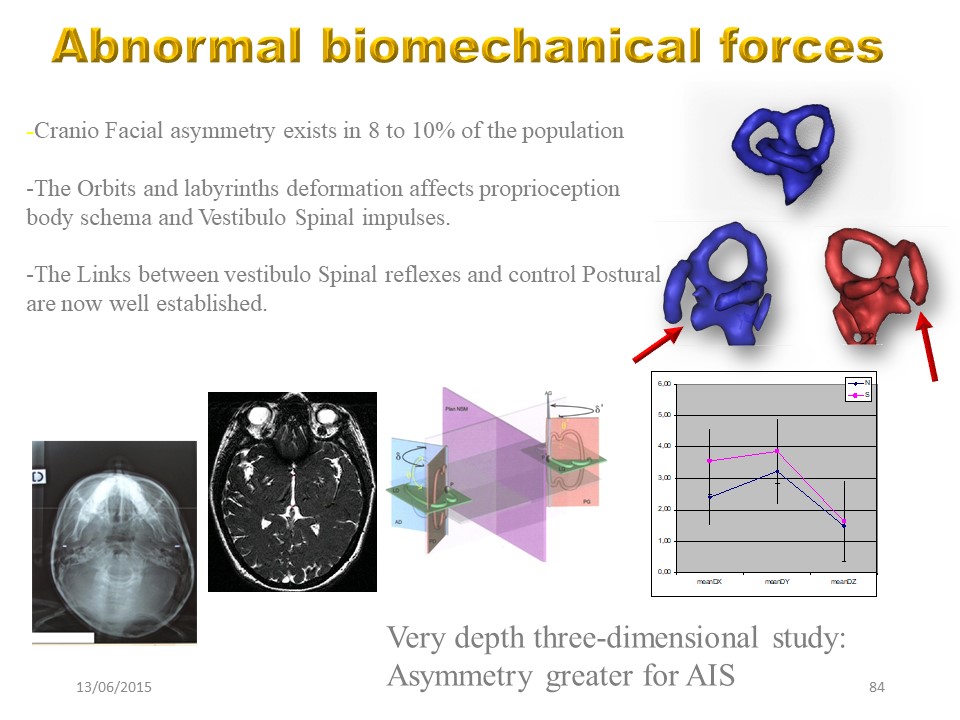 Les forces biomécaniques anormales s'associent à une déformation osseuse y compris au niveau du crâne, ce qui peut modifier le fonctionnement vestibulo-spinal.

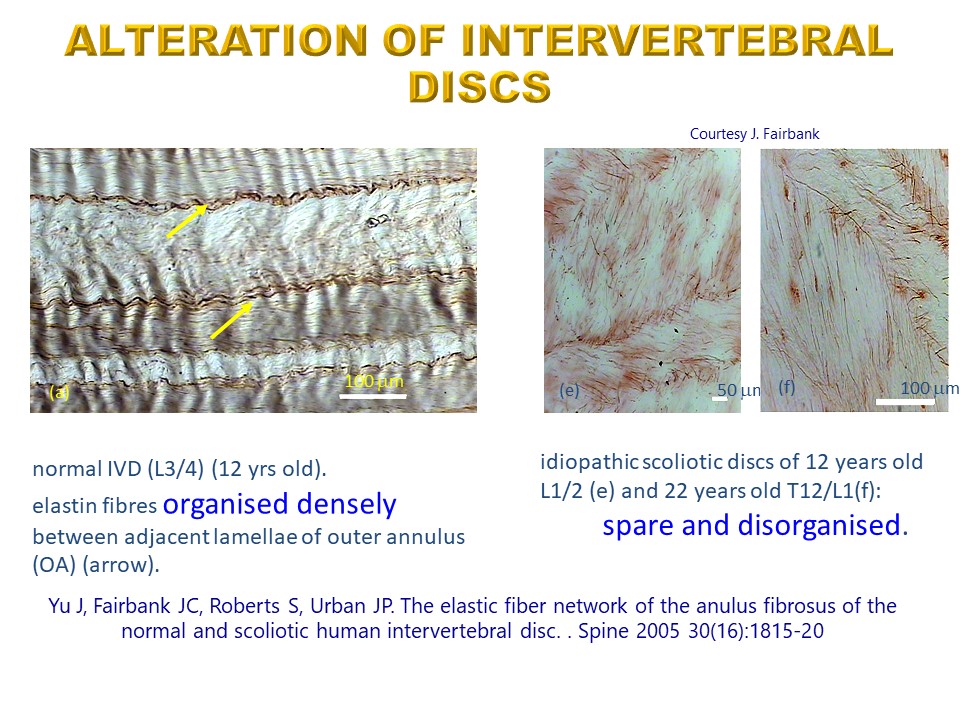 Les forces biomécaniques anormales vont également désorganiser les fibres élastiques à l'intérieur du disque intervertébral.

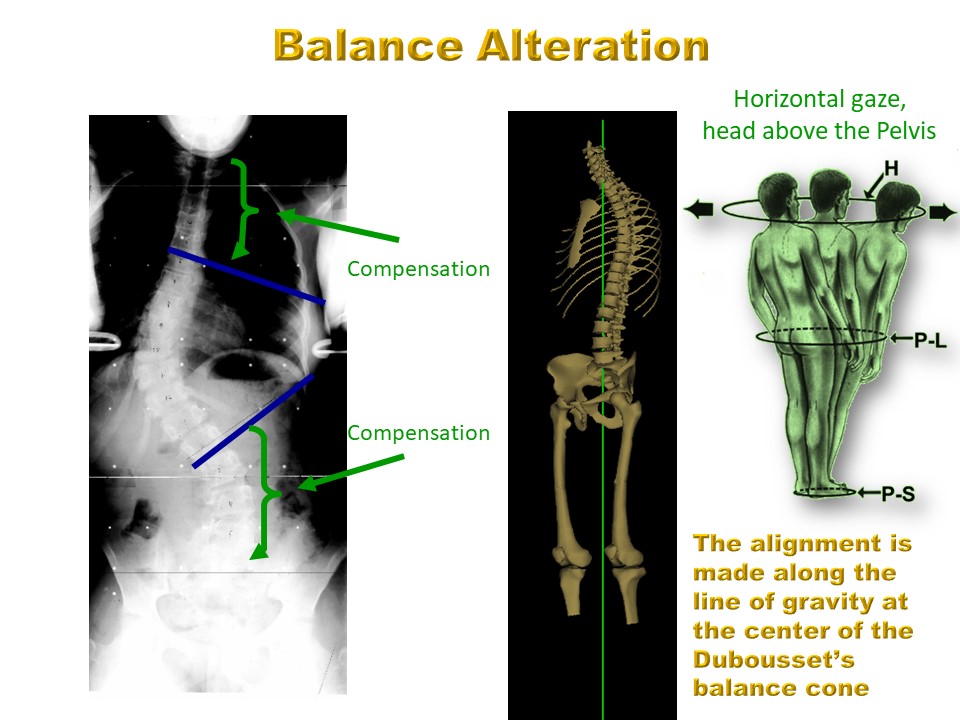 A cette phase les rigidités liées à la scoliose peuvent empêcher le système extra-pyramidal de fonctionner correctement, le tronc n'étant plus placé dans son cône d'équilibre.

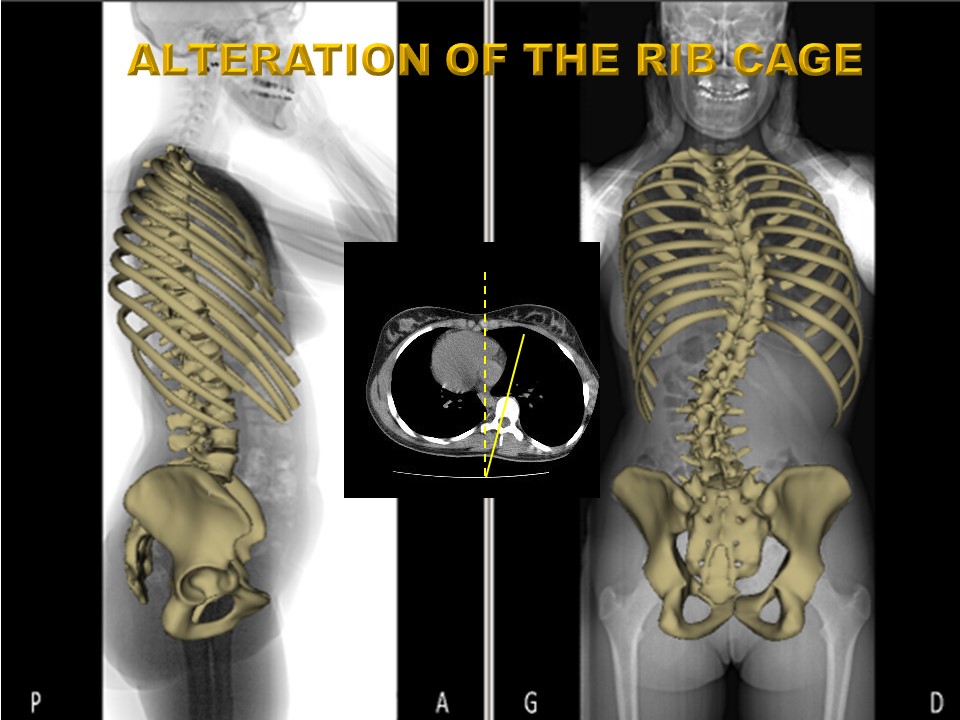 Les déformations ne concernent pas uniquement la colonne vertébrale, mais également la cage thoracique et le pelvis que se comporte comme une vertèbre.

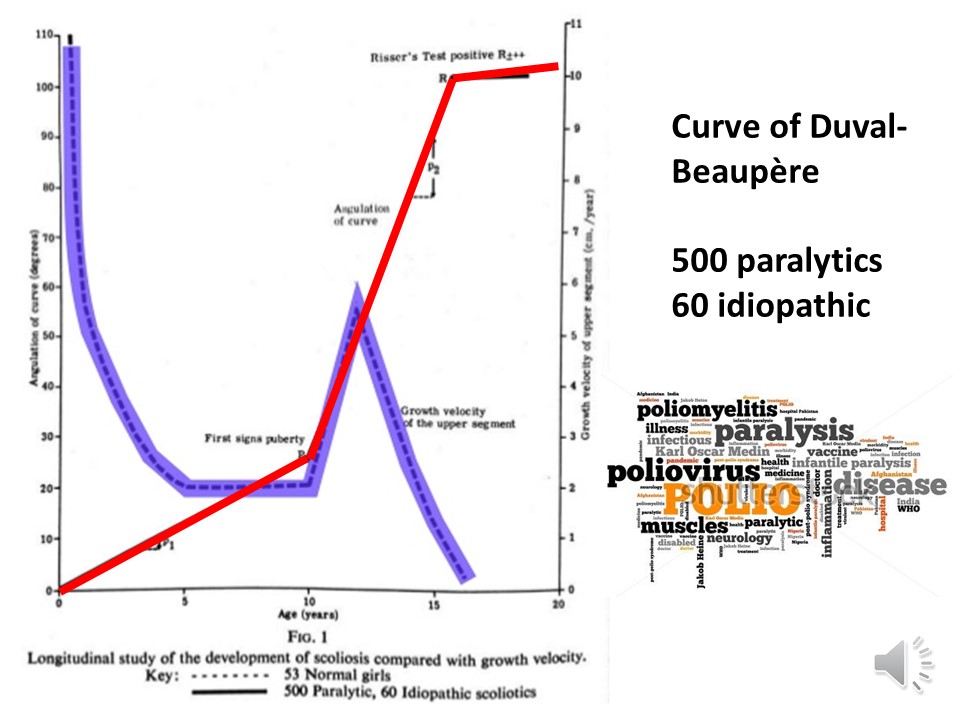 A cette phase, toutes les considérations étiologiques n'ont plus d'incidence sur l"évolution de la scoliose. La scoliose est considérée comme idiopathique lorsqu'il n'y a pas de maladie associée à la scoliose. Mais l'étiologie de la scoliose n'affecte pas la scoliose linéaire comme nous le constatons sur le diagramme de Duval-Beaupère, qui avait été réalisé initialement à partir de scolioses poliomyélitiques et confirmé secondairement pour les scolioses idiopathiques.

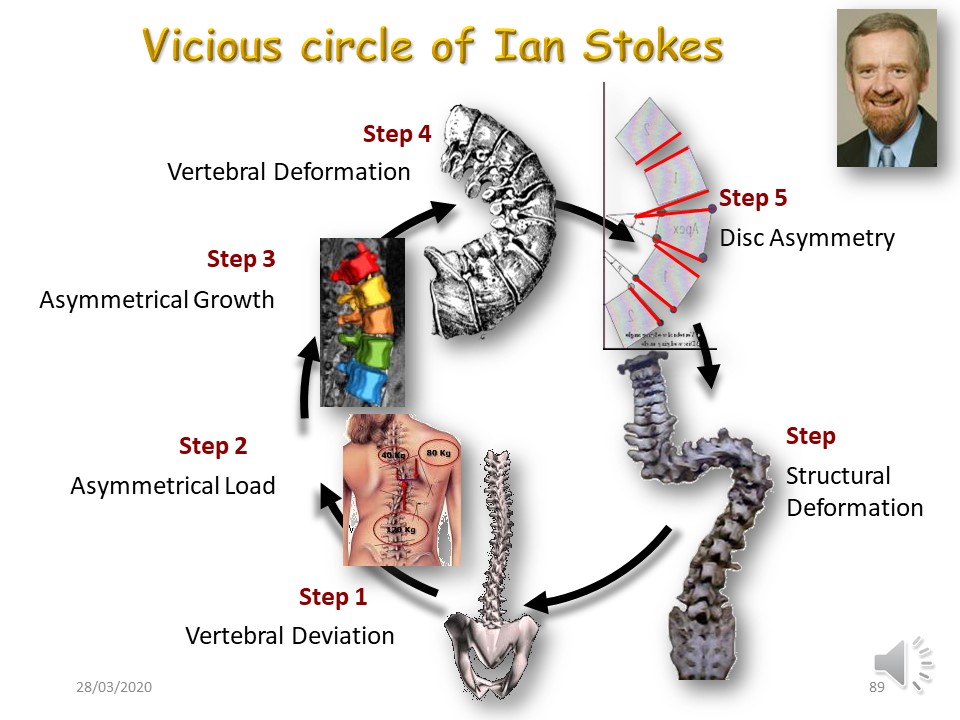 En effet, il s'agit alors d'un problème mécanique, avec implication successive ou simultanée de: 1. l'asymétrie de la tension paravertébrale, 2. la croissance asymétrique de la vertèbre apicale. 3. l'asymétrie du disque intervertébral.

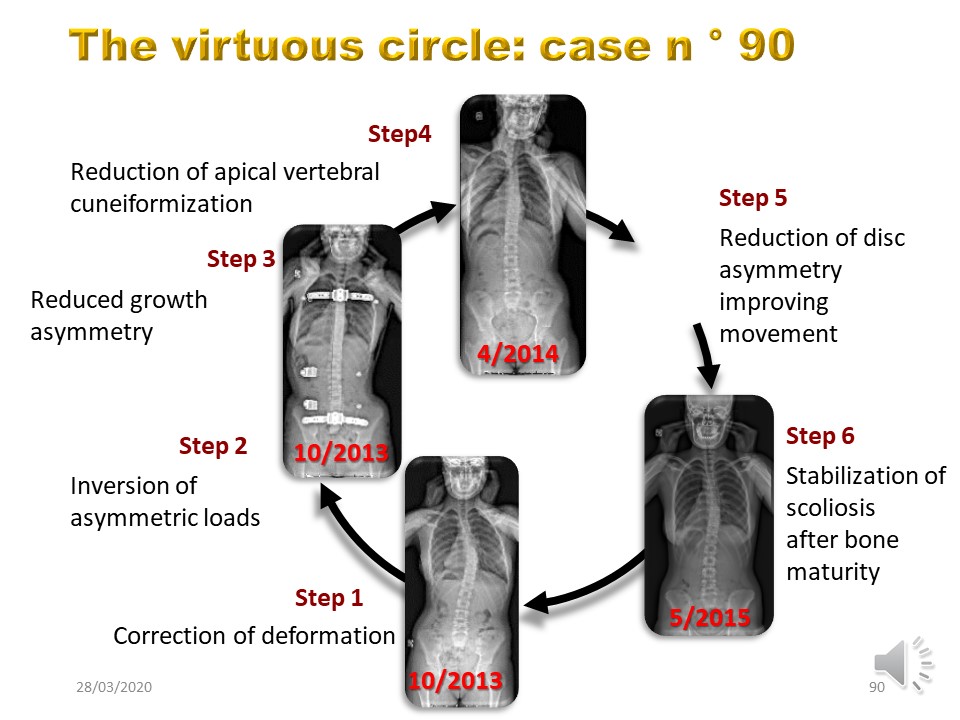 Pour obtenir un cercle vertueux, toutes les étapes doivent être prises en sens inverse: rééquilibrage des tensions paravertébrales, inversion des charges au niveau de la vertèbre apicale, réduction de l'asymétrie discale et stabilisation à maturité osseuse. Il s'agit non seulement de guider la croissance, mais de surcorriger la courbure et de maintenir le corset jour et nuit.

 L'environnement épigénétique est prédominant lors de l'initiation de la scoliose. La mélatonine contrôle la majorité des perturbations observées dans la scoliose idiopathique. En dessous de 20 ° d'angulation en croissance, l'évolution de la scoliose est chaotique. La physiothérapie est axée sur le système postural extra-pyramidal. Au delà de 20 ° d'angulation en période de croissance, l'évolution de la scoliose est linéaire, et la physiothérapie est axée en priorité sur les phénomènes mécaniques donc associée au port du corset. La reprogrammation du système postural doit s'effectuer en position corrigée.